이번 포스팅에서는 그래프라는 새로운 주제로 알고리즘과 자료 구조 분야의 영역을 다룰 것이다. 그래프가 무엇이고 그래프에서 사용하는 주요 용어와 예시를 통해 이야기 해보자. 또한 사진들을 보면서 그래프의 종류에는 어떤 것들이 있는지 배워보자.
1. Graph
1) Graph 란?
그래프란 무엇인가?
컴퓨터 공학을 전공하는 사람들은 꼭 한 번 들어봤을 법한 ‘Graph(그래프)’.
대학교 과정에서 데이터 구조, 알고리즘 등 주요 과목들에 자주 등장하는 용어이다.
그래프(Graph)
노드(N, Node)와 그 노드를 연결하는 간선(E, Edge)을 하나로 모아놓은 자료 구조
즉, 그래프란 연결되어 있는 객체 간의 관계를 표현할 수 있는 자료 구조이다.
백 번 말로 설명하기 보다는 직접 보면서 따라오는 것이 빠를거라고 생각하기 때문에 아래 예시를 함께 보자.
2) Graph 용어
그래프의 예시를 보며 그래프에 대해 좀 더 자세한 설명에 들어가기 전에,
그래프를 이야기 할 때 사용하는 용어에 대해 정리해보자.
- 정점(Vertex) : 위치라는 개념 (Node라고도 함)
- 간선(Edge) : 위치 간의 관계, 노드를 연결하는 선 (Link, Branch라고도 함)
- 인접 정점(Adjacent Vertex) : 간선에 의해 직접 연결된 정점
- 경로의 길이(Path Length) : 경로를 구성하는 데 사용된 간선의 수
- 단순 경로(Simple Path) : 경로 중에서 반복되는 정점이 없는 경우
- 사이클(Cycle) : 단순 경로의 시작 정점과 종료 정점이 동일한 경우
여기 까지가 그래프를 다루는 데에 정말 기본적으로 사용되어지는 용어들이다.
이 아래는 그래프의 종류에 따라 사용되어지는 용어들이다.
그래프의 종류에 따라 달리 사용되어질 뿐, 위와 마찬가지로 기본적인 용어들이기 때문에 숙지해 두자.
- 정점의 차수(Degree) : 무방향 그래프에서 하나의 정점에 인접한 정점의 수
- 진입 차수(In-Degree) : 방향 그래프에서 외부에서 오는 간선의 수 (내차수라고도 함)
- 진출 차수(Out-Degree) : 방향 그래프에서 외부로 향하는 간선의 수 (외차수라고도 함)
그래프에서 사용되어지는 용어들은 이것보다 더 많지만, 필자가 정말 기본적으로 알아둬야 할 그래프의 용어라고 생각되는 것은 여기까지이다. 여기까지 봤을 때, 한 가지 궁금증 ‘무방향 그래프는 뭐고 방향 그래프는 뭐지?’하는 질문이 떠오를 수 있는데, 이 부분은 아래의 그래프의 종류를 다루면서 함께 이야기 해보자.
3) Graph 예시
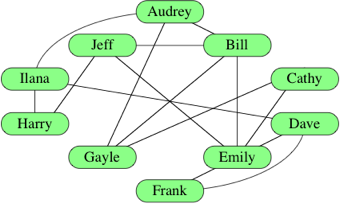그림1. 소셜 네트워크를 나타내는 그래프 예시
사진은 소셜 네트워크를 나타내는 그래프이다.
각 원을 사람의 이름(노드, N)으로 나타내고, 원 끼리 선(간선, E)이 이어지면 이어진 두 원의 사람끼리 서로 안다는 것을 나타낸다. 예를 들어 Frank를 설명하면 우리는 위 사진을 보고 Frank와 Emily는 서로 아는 사이이고, Frank와 Dave도 서로 아는 사이라는 것을 알 수 있다.
그래프의 용어 부분에서 언급했던 이야기를 해보자.
위 사진에서 정점은 총 10개의 이름들이고, 간선은 이 정점들을 잇고있는 모든 선들이 될 수 있다.
인접 정점은 정점의 종류 중 하나라고 생각하면 이해하기 쉬운데 정점 중에서도 간선에 의해 직접 연결된 정점을 인접 정점이라고 생각하면 된다. 그럼 위 사진에서 인점 정점은 뭐가 될까? 10개의 정점 모두 다른 정점과 간선에 의해 직접 연결되어있기 때문에 인접 정점이다.
경로의 길이를 살펴보자. Harry와 Emily의 경로 길이는 얼마일까?
Harry를 보면 Jeff를 거쳐 Emily와 연결되어 있다. 따라서 Harry와 Emily 사이에 간선은 2개이고 경로의 길이는 2가 된다. 하지만 사실 Harry와 Emily의 경로의 길이를 2로 정하는 것은 정확하지 않은 표현이다.
Harry와 Emily를 다시 보면, Harry에서 Ilana와 Dave를 거쳐 Emily로 가는 경로도 가능한데 이렇게되면 경로의 길이는 3이 된다. 따라서 우리는 경로의 길이를 살펴볼 때 보통 최소경로의 길이(Shortest Path Length) 혹은 최장경로의 길이(Longest Path Length)로 경로를 정한 뒤 구하게 된다.
위 그래프의 정점의 차수에 대해 이야기 하면, 위 그래프는 간선에 방향이 없는 무방향 그래프이기 때문에 진입 차수와 진출 차수를 따로 나누지 않는다. 무방향 그래프와 방향그래프에 대한 차이 설명은 아래 그래프의 종류에서 더 자세히 다루도록 하고, 일단은 위 그래프가 무방향 그래프라 생각하고 정점의 차수에 대해 알아보자.
정점의 차수는 인접 정점이 몇 개 인지로 알 수 있다. Emily의 차수를 알아보면, Emily는 Bill, Cathy, Dave, Jeff, Frank와 인접해 있다. 따라서 Emily의 차수는 5가 된다.
그래프에서 사용되는 용어들을 한 가지 그래프의 예시를 보면서 더 자세하고 직관적으로 알아보았다.
이제 그래프의 여러가지 종류를 보면서 그래프에 대한 개념의 폭을 넓혀 보도록 하자.
2. Graph의 종류
그래프의 종류는 정말 다양하다.
그 중에서 우리가 이번에 다룰 그래프는 무방향 그래프와 방향 그래프, 가중치 그래프이다.
그래프 중에서도 정말 자주 언급되는 대표적인 그래프이며, 꼭 알아둬야 할 그래프이다.
1) 무방향 그래프 (Undirected Graph)
그림1. 무방향 그래프
무방향 그래프는 위 예시에서도 한 번 언급했는데, 간선이 양방향인 그래프이다.
이름은 방향이 없음을 나타내는 ‘무방향’인데 양방향을 나타낸다고하니 당황스러울 수 있는데, 간선이 양방향임을 내포해 방향이 존재하지 않는다고 생각할 수도 있고, 간선을 그릴 때 방향을 표현하지 않기 때문에 무방향 그래프라고 이야기하는 것 같다. (필자의 뇌피셜)
정점 A와 정점 B를 연결하는 간선은 (A, B)와 같이 정점의 쌍으로 표현한다.
방향이 존재하지 않기 때문에 (A, B)와 (B, A)는 동일
2) 방향 그래프 (Directed Graph)
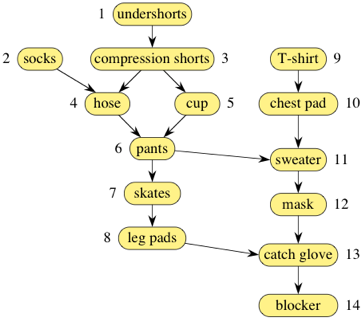그림2. 방향 그래프
방향 그래프는 간선의 방향성이 존재하는 그래프이다.
간선의 방향성이 존재하기 때문에 순서를 표현하는 데에도 사용되어질 수 있으며, 한 정점을 떠나(Leave) 다른 정점으로 들어간다(Enter)고 이야기한다.
정점 A에서 정점 B로 향하는 간선을 <A, B>로 표현한다.
방향성이 있기 때문에 <A, B>와 <B, A>는 다름
3) 가중치 그래프 (Weighted Graph)
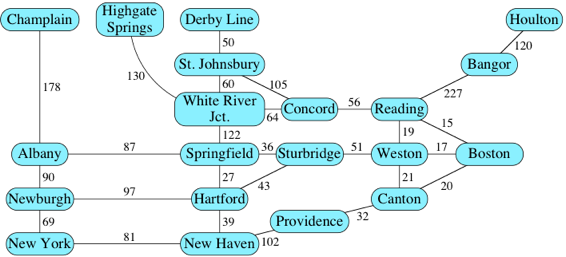그림3. 가중치 그래프
가중치 그래프는 간선에 비용이나 가중치가 할당된 그래프이다.
같은 용어로 네트워크(Network)라고도 하며, 간선 사이의 가중치를 이용해서 위에서도 언급했던 최소 경로(Shortest Path)나 최장 경로(Longesg Path)가 고려되어 질 수 있다.
3. Reference
- 블로그 사이트 : [자료구조] 그래프(Graph)란
- 학습 사이트 : [Khan Academy] 그래프 설명하기