알고리즘을 공부하다보면 Dynamic Programming Algorithm이라는 것에 대해 배운다.
한국어로 하면 ‘동적 프로그래밍’인데, 실제로 사용하는 것을 보면 전혀 다이나믹 하지 않다.
이번 포스팅에서는 Dynamic Programming이 어떤 알고리즘 기법인지 보고,
이 알고리즘이 Recursive 알고리즘과 비교해서 얼마나 효율적인지를 이야기 해보자.
1. Recursive Algorithm
Dynamic Programming에 대한 이야기를 하기 전에, 먼저 Recursice Algorithm을 알아보자.
1) Recursion 이란?
Recursion
자신을 정의할 때 자기 자신을 재참조하는 방법
Recursion(재귀)란 위 정의에서 말하는 것과 같다.
말이 조금 어려울 수 있어 재귀함수(Recursive funtion)를 예로 이야기하면,
함수를 정의할 때 자신의 함수를 다시 사용하는 함수를 재귀함수라고 한다.
2) Recursive Algorithm
위에서 이야기 했듯이, Recursion은 자신을 정의할 때 자기 자신을 재참조 하는 방법이다.
따라서, Recursive Algorithm은 계속해서 자기 자신을 재참조하는 방식으로 프로그래밍이 이루어진다.
여기에서 ‘그럼 영원히 끝나지 않는거 아니야?’라는 생각이 떠오를 수 있는데,
Recursive Algorithm은 기본적으로 ‘base case’와 ‘recursive case’로 나뉜다.
따라서 recursive case에서 자신을 재참조 하다가 어떤 조건을 만족하는 순간 base case로 들어가 끝이 난다.
Recursive Algorithm은 보통 ‘Top-Down Approach’ 방식으로 작동한다.
2. Dynamic Programming Algorithm
Dynamic Programming은 실제로 다이나믹 하지 않다.
또한 여기서 이야기하는 프로그래밍이 컴퓨터 프로그래밍이 아니라 테이블을 만든다는 뜻이다.
그래서 Dynamic Programming을 ‘동적 프로그래밍’ 대신 ‘기억하기 프로그래밍’이라고도 한다.
1) Dynamic Programming Algorithm
Dynamic Programming(이하 DP)을 설명하기 위해서는 Memoization에 대해 알아야 한다.
Memoization은 일종의 테크닉 중 하나로, 계산된 값을 버리지 않고 저장하는 것이다.
DP는 이 Memoization 테크닉을 사용한다.
따라서 DP를 Memoization과 연관지어 아래와 같이 이야기 할 수 있다.
계산된 값을 저장해 놓고 있다가, 필요한 경우 계산 없이 호출하는 알고리즘 방법
DP 알고리즘은 쉽게 말해서 반복적으로 계산되는 것들의 계산 횟수를 줄이기 위해서 이전에 계산했던 값을 저장해 두었다가 나중에 재사용하는 방법이다. 이전에 계산했던 값을 테이블을 만들어 저장하고, 같은 계산을 해야할 때 계산하지 않고 저장했던 값을 사용하기 때문에 기억하기 프로그래밍이라고도 하는 것이다.
또한 DP 알고리즘은 Recursive Algorithm과는 다르게 보통 ‘Bottom-Up Approach’ 방식으로 작동하는데, ‘Top-Down Approach’ 방식으로 코드를 수정할 수도 있다.
3. Simple Example
말로 설명하는 것 보다는 직접 코드를 보면서 이해하는 것이 쉽기 때문에 간단한 예제를 보자.
아래 예제는 피보나치 수열을 구하는 코드를 각각 Recursive Algorithm과 Dynamic Programming Algorithm을 사용해서 프로그래밍한 것이다.
1) Recursive Algorithm Example
1
2
3
4
int fib(int n) {
if (n < 2) return n ;
else return fib(n - 1) + fib(n - 2) ;
}
위의 코드를 보면 알겠지만 base case if (n < 2)에서는 단순히 n을 리턴하고,
recursive case else에서는 자신의 함수를 다시 불러 들임으로써 재귀함수를 완성한다.
n을 2로 예를 들어보면, 처음에 fib함수에 들어왔을 때 recursive case로 들어간다.
그러면 fib(1) + fib(0)을 리턴하게 되므로 fib(1)부터 다시 함수를 불러들여 계산하면,
n이 1이기 때문에 base case로 들어가게돼 1을 리턴하고 fib(0)도 마찬가지로 0을 리턴한다.
따라서 fib(1) + fib(0)는 (1 + 0 = 1)이 되어서 2번째 피보나치 수열은 1이 되는 것이다.
Recursive Algorithm을 설명하면서 ‘Top-Down Approach’ 방식을 언급했었는데,
방금도 설명했듯 큰 수(2)에서 점점 작은 수(1, 0)를 구하는 방식으로 진행되기 때문에 ‘Top-Down Approach’ 이다.
2) Dynamic Programming Algorithm Example
1
2
3
4
5
6
7
8
9
10
11
int fib(int n) {
int * fib_table = (int *)malloc(sizeof(int) * (n + 1)) ;
fib_table[0] = 0 ;
fib_table[1] = 1 ;
for (int i = 2; i < n + 1; i++)
fib_table[i] = fib_table[i - 1] + fib_table[i - 2] ;
return fib_table[n] ;
}
위 코드를 보면, Recursive Algorithm과 다른 점은 처음에 계산된 값을 저장할 테이블을 생성한다는 것이다.
그리고 0번째 피보나치 수열과 1번째 피보나치 수열에 각각 자기 자신을 넣어주는데,
이 부분이 Recursive Algorithm에서는 base case와 같은 부분이라고 이야기 할 수 있다.
그 후 2번째 피보나치 수열부터 테이블에 저장된 값을 불러와 더한 값을 다시 테이블에 저장해주는 식으로 계산된다. 그리고 앞에서도 이야기 했듯이, DP는 보통 ‘Bottom-Up Approach’ 방식(0, 1부터 점점 늘어나는 식)으로 작동한다.
3) 전체 코드
피보나치 수열을 구하는 코드를 직접 돌려보고 싶은 분들을 위해 각각 Recursive Algorithm과 Dynamic Programming Algorithm 방법으로 짠 코드를 공유한다. 각 코드는 C언어로 짠 코드이고, 아래 코드를 그대로 복사해서 c파일을 만들어 컴파일해서 돌려보면 될 것이다.
- Recursive Algorithm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int fib(int n) ;
int main(int argc, char * argv[]) {
if(argc == 1) {
printf("\nThis program is computing Fibonacci number.\n") ;
printf("Usage : ./<executable> <n>\n") ;
printf(" n is the number which you want to compute Fibonacci number.\n\n") ;
} else if (argc == 2) {
int n = atoi(argv[1]) ;
if (strcmp(argv[1], "0") != 0 && n == 0) { printf("err: No command!\n") ; return 0 ; }
int fib_num = fib(n) ;
printf("%d's Fibbonacci number : %d\n", n, fib_num) ;
} else printf("err: No command!\n") ;
}
int fib(int n) {
if (n < 2) return n ;
else return fib(n - 1) + fib(n - 2) ;
}
- Dynamic Programming Algorithm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int fib(int n) ;
int main(int argc, char * argv[]) {
if(argc == 1) {
printf("\nThis program is computing Fibonacci number.\n") ;
printf("Usage : ./<executable> <n>\n") ;
printf(" n is the number which you want to compute Fibonacci number.\n\n") ;
} else if (argc == 2) {
int n = atoi(argv[1]) ;
if (strcmp(argv[1], "0") != 0 && n == 0) { printf("err: No command!\n") ; return 0 ; }
int fib_num = fib(n) ;
printf("%d's Fibbonacci number : %d\n", n, fib_num) ;
} else printf("err: No command!\n") ;
}
int fib(int n) {
int * fib_table = (int *)malloc(sizeof(int) * (n + 1)) ;
fib_table[0] = 0 ;
fib_table[1] = 1 ;
for (int i = 2; i < n + 1; i++)
fib_table[i] = fib_table[i - 1] + fib_table[i - 2] ;
return fib_table[n] ;
}
4. Efficiency
간단한 피보나치 예제로 각각의 알고리즘이 어떤 방법인지는 대충 감을 잡았을 것이다.
그럼 여기서 더 나아가 살펴봐야 할 것이 효율성인데, DP 알고리즘에서 계속해서 강조하는 것이 ‘반복되는 계산을 피하기위해서 값을 저장한다’는 것이다. 이 말을 들었을 때 ‘그러면 Recursive 알고리즘은 반복되는 계산이 있나?’하는 의문이 들 수 있는데, 맞다. Recursive 알고리즘은 반복되는 계산이 나올때마다 다시 계산하기 때문에 DP보다 무척 비효율적이다.
아래 사진을 보면서 이야기 해보자.
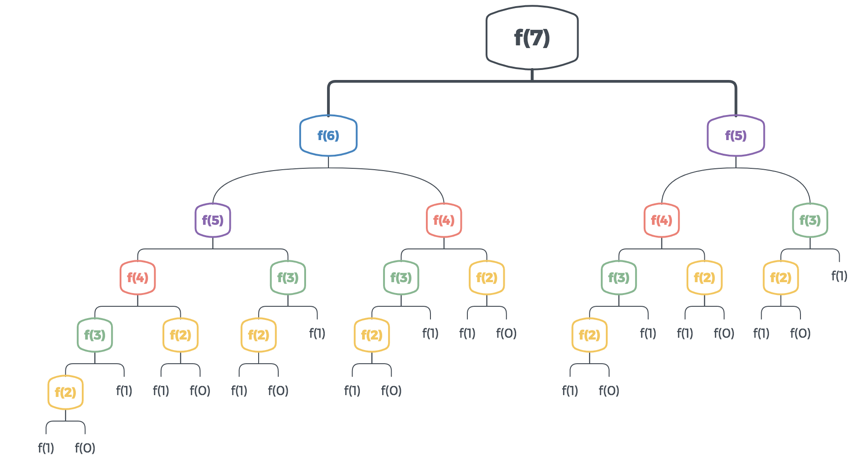그림1. 피보나치 수열 7의 Recursive Tree
위 사진은 Recursive 알고리즘을 적용했을 때, 피보나치 수열 7의 Recursive Tree이다.
여러가지 색으로 이루어져있는데, 반복되는 계산끼리 같은 색으로 표현되어 있는 것이다.
따라서 Recursive 알고리즘은 같은 색의 갯수만큼 반복 계산을 하는 반면에, DP는 계산한 값을 저장해두기 때문에 위와 같은 계산을 반복하지 않는다. 위 사진은 피보나치 수열 7을 예로 든 것인데, 반복 계산은 피보나치 수열의 숫자가 커질 수록 더욱 극명하게 드러난다.
5. Combination Example
위에서 이론적인 효율성 부분에 대해서 이야기 해보았다.
하지만 실질적으로 DP 알고리즘이 얼마나 효율적인지 체감하기에는 조금 어려움이 있을 것이다.
그래서 필자가 확실히 체감할 수 있는 예제를 준비해 보았다.
아래 코드는 조합(Combination)의 경우의 수를 구하는 프로그램이다.
그리고 Recursive와 DP 알고리즘의 효율성을 비교하기 위해 조합의 경우의 수를 구하는 데에 얼마나 많은 시간이 걸리는지 각 알고리즘 별로 시간을 표시해 보았다.
직접 코드를 돌려보면서 그 차이를 알고싶은 분들은 아래 코드를 그대로 복사해 컴파일해서 돌려볼 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
void print_help() ;
long long recursive_algorithm(int n, int k) ;
long long dynamic_programming_algorithm(int n, int k) ;
int main(int argc, char * argv[]) {
if(argc == 1) print_help() ;
else if (argc == 4) {
char * option = argv[1] ;
int n = atoi(argv[2]) ;
int k = atoi(argv[3]) ;
if (n >= 0 && k <= n) {
clock_t start, finish ;
double duration = 0.0 ;
printf("Computing %dC%d...\n", n, k) ;
if (strcmp(option, "-r") == 0 || strcmp(option, "-b") == 0) {
start = clock() ;
long long result = recursive_algorithm(n, k) ;
finish = clock() ;
duration = (double)(finish - start)/CLOCKS_PER_SEC ;
printf("Recursive Algorithm: %lli | time : %f sec\n", result, duration) ;
}
if (strcmp(option, "-d") == 0 || strcmp(option, "-b") == 0) {
start = clock() ;
long long result = dynamic_programming_algorithm(n, k) ;
finish = clock() ;
duration = (double)(finish - start)/CLOCKS_PER_SEC ;
printf("Dynamic Programming: %lli | time : %f sec\n", result, duration) ;
}
} else printf("err: n is smaller than k!\n") ;
} else printf("err: No command!\n") ;
return 0;
}
long long recursive_algorithm(int n, int k) {
if (k == n || k == 0) return 1 ;
else return recursive_algorithm(n-1, k-1) + recursive_algorithm(n-1, k) ;
}
long long dynamic_programming_algorithm(int n, int k) {
long long ** combination ;
long long answer ;
combination = (long long **)malloc(sizeof(long long *) * (n+1)) ;
for(int i = 0; i < n + 1; i++)
combination[i] = (long long *)malloc(sizeof(long long) * (i + 1)) ;
for (int i = 0; i < n + 1; i++) {
for(int j = 0; j <= i && j != k + 1; j++) {
if(i == j || j == 0) combination[i][j] = 1 ;
else combination[i][j] = combination[i-1][j-1] + combination[i-1][j] ;
}
}
answer = combination[n][k] ;
for (int i = 0; i < n + 1; i++) free(combination[i]) ;
free(combination);
return answer ;
}
void print_help() {
printf("This program is computing Combination.\n") ;
printf("Usage: ./<excutable> <option> <n> <k>\n") ;
printf("option:\n") ;
printf(" -r Recursive Algorithm\n") ;
printf(" -d Dynamic Programming Algorithm\n") ;
printf(" -b Both and comparing\n") ;
}
직접 컴파일해서 돌려보면 아래와 같은 결과를 볼 수 있다.
아래는 \(\begin{align*} \phantom{}_{20}\mathrm{C}_{5} \end{align*}\) (20개 중 순서에 상관없이 5개를 선택했을 때 경우의 수)일 때의 경우의 수와 계산하는 데 걸리는 시간이다.
1
2
3
Computing 20C5
Recursive Algorithm: 15504 | time : 0.000128 sec
Dynamic Programming: 15504 | time : 0.000028 sec
위의 경우에서 시간에 큰 차이를 느끼지 못하신 분들은 아래의 경우도 보자.
아래는 \(\begin{align*} \phantom{}_{40}\mathrm{C}_{20} \end{align*}\) 일 때의 경우의 수와 계산하는 데 걸리는 시간이다.
1
2
3
Computing 40C20
Recursive Algorithm: 137846528820 | time : 619.346706 sec
Dynamic Programming: 137846528820 | time : 0.000108 sec
위 경우를 보면 정말 큰 차이를 느낄 수 있을 것이다.
Recursive의 경우는 10분이 넘는 시간이 걸리는데, DP의 경우 단 0.001초도 걸리지 않는다.
직접 조합을 예로 들어서 각 알고리즘 별로 돌려보니 효율성 측면에서 확실히 차이가 큰 것을 체감할 수 있었을 것이다. 그리고 반복되는 계산이 많다면 저장해두고 사용하는 것이 시간적 측면에서 얼마나 많은 비용을 줄여주는지를 알 수 있었을 거라 믿는다.
6. GitHub Repository
이번 포스팅에서 설명했던 예제 코드들은 깃헙에 올려두었으니 필요하신 분들은 아래 링크를 참고하시길.